Un ejercicio de lógica matemática ha provocado más de un  millón de comentarios en Facebook y se volvió viral. Al parecer, hay más de un camino para resolverlo, según un artículo publicado este sábado por El País de España. En realidad, hay dos formas de hacerlo, aparentemente.

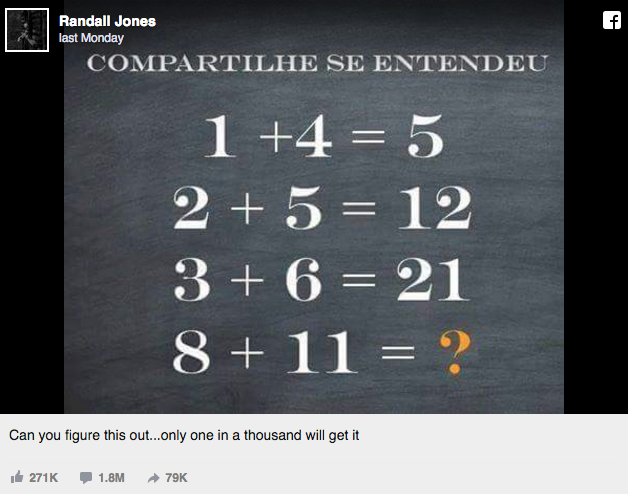
En la primera, un grupo de personas llega al resultado combinando las líneas e ignorando los signos "+" e "=". Es decir, si se suma al 5 de la primera línea el 2 y el 5 de la segunda, tenemos un 12. Si a eso se añade un 3 y un 6 de la tercera, se obtiene el 21. 

Así, para la cuarta línea se suma al 21 el 8 y el 11 y se llega al número 40.

Pero si se respeta el signo igual y se le asigna al signo de "+" a alguna operación que sea compatible con las tres primeras líneas solo hará falta aplicar esa operación a la cuarta línea. Así, podríamos interpretar "a + b" como: a x (1 + b). 

Entonces tendríamos:
1 + 1 x 4 = 5

2 + 2 x 5 = 12

3 + 3 x 6 = 21

8 + 8 x 11 = 96

Pero lo cierto, como resalta el artículo de El País, que "desde el punto de vista matemático, y más allá de las interpretaciones que podamos dar a la forma de operar números o a la interpretación más o menos excéntrica de un signo, es conocido que una secuencia numérica podría seguir de muchas maneras".

De hecho, existe el proyecto OEIS, fundada por el matemático inglés Neil Sloane, que una suerte de Wikipedia de las secuencias o sucesiones de números enteros en internet.  Por ejemplo, si ponemos los tres o cuatro números con los que podría empezar cualquier secuencia, te dice a qué sucesiones catalogadas pertenecen, cómo empiezan, cómo siguen, comentarios, utilidades y dónde buscar más información.

El País hizo la prueba e ingresó los números de la secuencia de la publicación viral en Facebook (5, 12 y 21, sin los primeros términos). El resultado: 67 secuencias de números distintas en las que 5, 12 y 21 son términos consecutivos. 

"El primer resultado nos dice que los números 5, 12 y 21 son los primeros tres resultados positivos de hacer “el cuadrado menos cuatro” (n^2 - 4)", se lee en el artículo de José Ángel Murcia.